|
Kriterien |
Homogene Gleichungssysteme
A·x = 0 |
Inhomogene Gleichungssysteme
A·x = c |
|
Generell gilt
|
Es gibt eine oder unendlich viele Lösungen. Es existiert mindestens die triviale Lösung x = 0 (Nullvektor).
|
Es gibt keine, eine oder unendlich viele Lösungen. Der Nullvektor x = 0 kommt als Lösung nicht vor.
|
Rang(A) 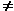 Rang(A|c)
Rang(A|c) |
Dieser Fall kommt nicht vor, denn es gilt immer: Rang(A) = Rang(A|0) |
Keine Lösung. Denn Rang(A) 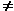 Rang(A|c) bedeutet, dass eine der Gleichungen äquivalent zu 0 = 1 ist, und damit unerfüllbar. Rang(A|c) bedeutet, dass eine der Gleichungen äquivalent zu 0 = 1 ist, und damit unerfüllbar.
|
|
Rang(A) = Rang(A|c) |
Lösbar. Siehe Rang(A) = n bzw. Rang(A) < n. |
Lösbar. Siehe Rang(A) = n bzw. Rang(A) < n.
|
Rang(A) = n
( |A| |A| 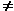 0, 0,
d.h. A regulär
für (n,n)- Gl.systeme)
|
Eindeutige Lösung: die triviale Lösung x = 0 , die immer existiert.
A ist invertierbar.
|
Eindeutige Lösung: ein konstanter Lösungsvektor.
A ist invertierbar.
|
Rang(A) < n
( |A| = 0, |A| = 0,
d. h. A singulär für (n,n)- Gl.systeme) |
Zusätzlich zur trivialen Lösung gibt es unendlich viele nichttriviale Lösungen, die sich aus n - Rang(A) linear unabhängigen Lösungsvektoren ergeben.
A ist nicht invertierbar. Das Gleichungssystem ist unterbestimmt (eine oder mehrere Zeilen lauten 0 = 0). |
Unendlich viele Lösungen. Sie ergeben sich aus n - Rang(A) linear unabhängigen Lösungsvektoren und
einem speziellen konstanten Lösungsvektor.
A ist nicht invertierbar. Das Gleichungssystem ist unterbestimmt (eine oder mehrere Zeilen lauten 0 = 0).
|
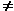 Rang(A|c)
Rang(A|c)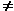 Rang(A|c) bedeutet, dass eine der Gleichungen äquivalent zu 0 = 1 ist, und damit unerfüllbar.
Rang(A|c) bedeutet, dass eine der Gleichungen äquivalent zu 0 = 1 ist, und damit unerfüllbar.
 |A|
|A| 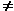 0,
0,
 |A| = 0,
|A| = 0,